Keyboard Shortcuts?f

×
  • →Next step
  • ←Previous step
  • ↓Skip this slide
  • ↑Previous slide
  • mShow slide thumbnails
  • tShow transcript (+SHIFT = all transcript)
  • nShow notes (+SHIFT = all notes)

Please be cautious in using the transcripts.

They were created mechanically and have mostly not been checked or revised.

Here is how they were created:

  1. live lecture recorded;
  2. machine transcription of live recording;
  3. ask LLM to clean up transcript, and link to individual slides.

This is an error-prone process.

Click here and press the right key for the next slide.

(This may not work on mobile or ipad. You can try using chrome or firefox, but even that may fail. Sorry.)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (or add '?notes' to the url before the #)

Press m or double tap to slide thumbnails (menu)

Press ? at any time to show the keyboard shortcuts

 

What Are Preferences?

insert-transcript#f465c4f0-3e24-4051-9bd9-f49d1af3b7b8-here

This book has ‘a philosophical end: elucidation of the notions of subjective probability and subjective desirability or utility’

(Jeffrey, 1983, p. xi)

ok, so how is this done?
subjective probabilities and preferences known actions inferred known actions subjective probabilities and preferences inferred
When we were looking at the representation, I was presenting decision theory as if we know subjective probabilities and preferences.
And I just say, oh, you know, how much do you prefer this amount of broccoli over that amount of broccoli? And then we can work out what actions is most rational for you to do.
That's the forward way of looking at it.
But what Ramsey Frank Ramsey famously showed. Is that you can actually go the other way.
So this is Ramsey's famous representation theorem.
If you observe somebody's actions, you can infer their subjective probabilities and preferences.
Why is this important?
Because it shows that those subjective probabilities and preferences are things which are characterised by the theory. Formally speaking, the theory can take for granted the idea that there are actions and outcomes, and it can tell you what it is for somebody to have a particular preference ranking, and it can tell you what it is for somebody to have particular subjective expectations or beliefs.
So this direction is super important to us.
If we can observe actions and then assign subjective probabilities and preferences, we've shown that it's reasonable to treat those things as constructs of decision theory.
insert-transcript#b1bed794-9173-4bb2-96c0-57052195d749-here
Difference scenario, bananas or chocolate. Both subjective probabilities and preferences unknown to us.
insert-transcript#3e18a6e5-b0fa-4380-8a3c-be265aaafa59-here
Subject opens the red door. What can we conclude? That they like bananas more than chocolate? Not necessarily.
insert-transcript#75276c03-8ea2-445a-859f-47dd10b2ab1b-here
I mean, if we knew their subjective probabilties, then maybe we could conclude that they like bananas more than chocolate.
insert-transcript#8db1d0a3-4b18-4f4d-bb44-2ab9db219ef7-here
But we don’t know their subjective probabilities. Suppose their subjective probabilities were like this. Then their choice does not tell us that they prefer bananas to chocolate.

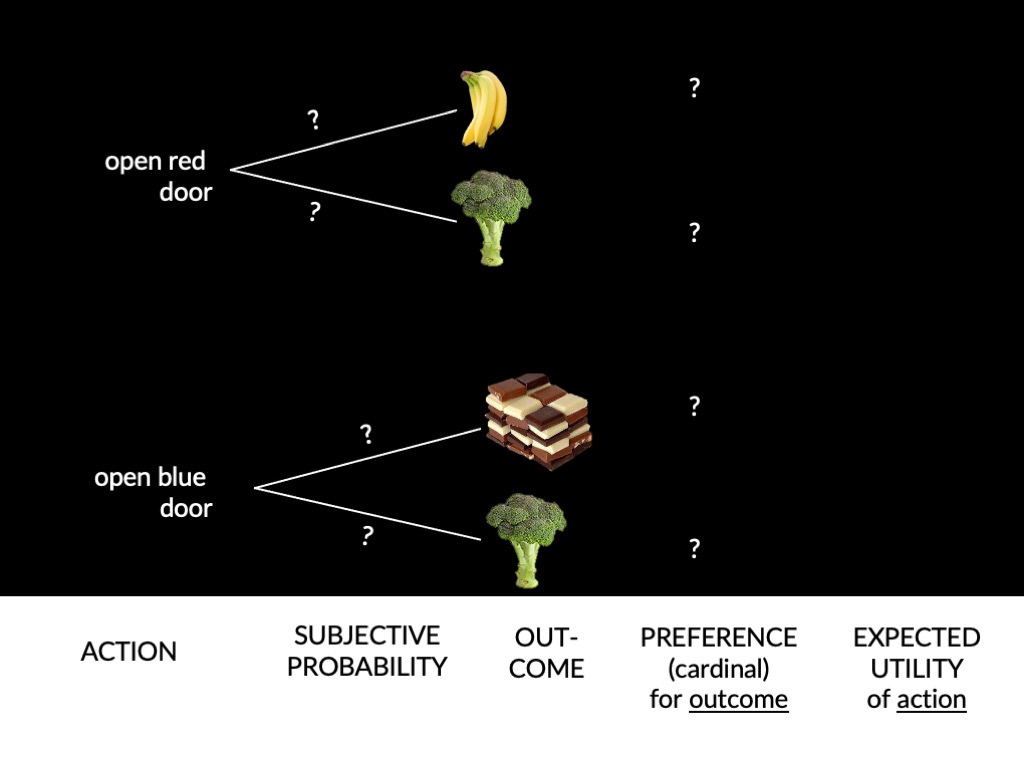
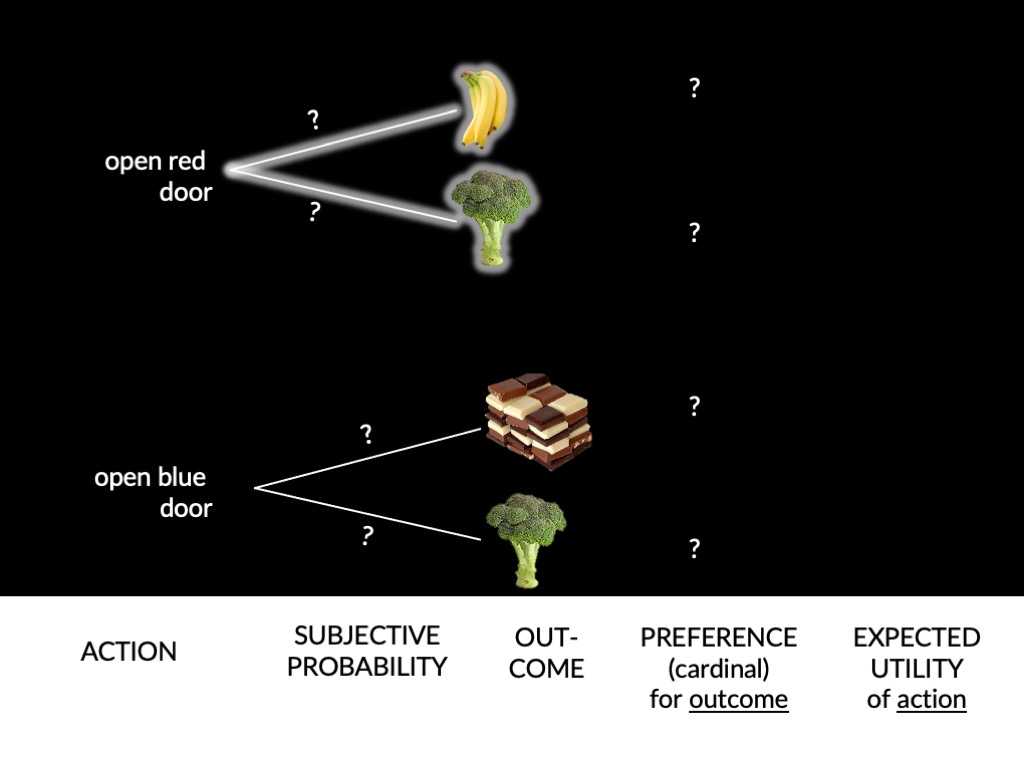
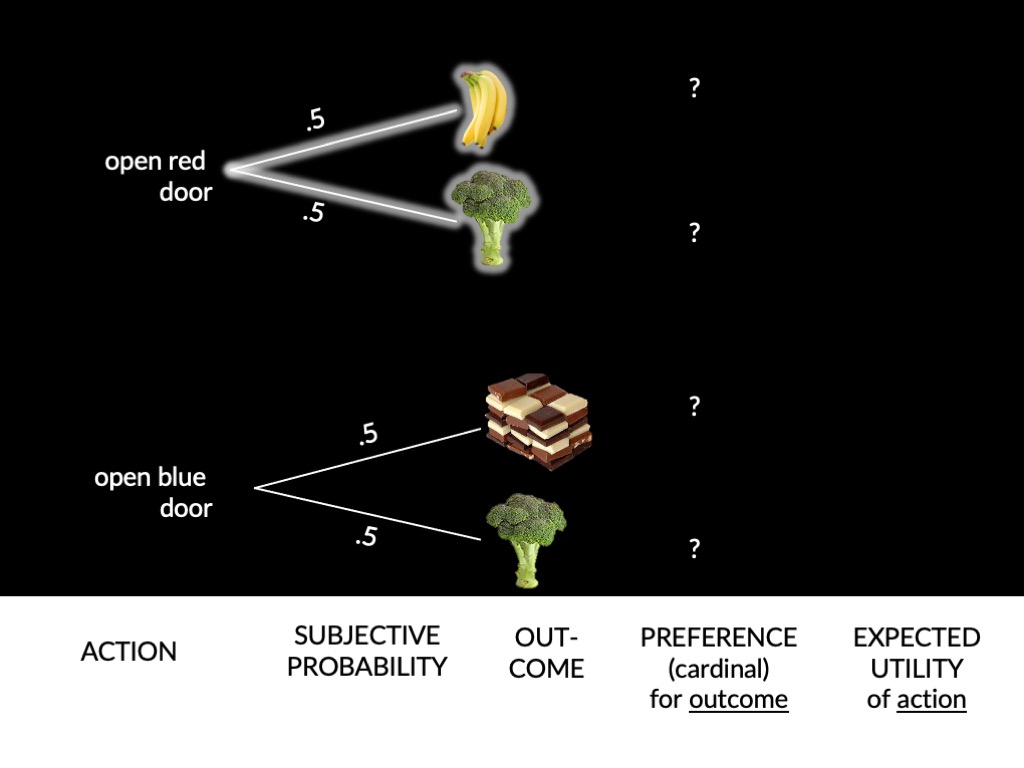
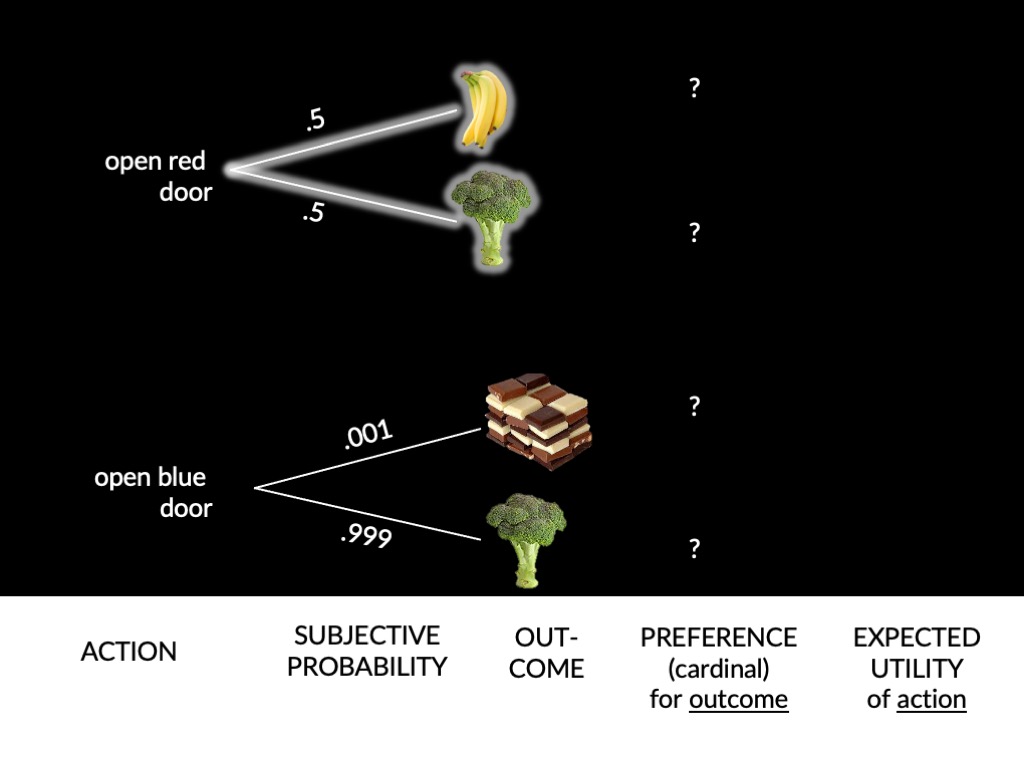
cannot infer preferences unless we know subjective probabilities

insert-transcript#94314d90-e97e-49de-a91b-f00f9de16cab-here
revealed preferences Importance: transition from externally given criterion

‘the revealed preference revolution of the 1930s (Samuelson, 1938)

... replaced the supposition that people are attempting to optimize any externally given criterion (e.g., some psychologically interpretable motion of utility, perhaps to be quantified in units of pleasure and pain).

Chater (2014)

insert-transcript#bfd18e48-c54f-4347-8403-7d46e434489a-here
Up to this point we regarded decision theory as forward looking ...
TODO: Can’t remember how you figure out that agent is not indifferent between A and B. (Is this an axiom?)
ANS?: as long as there is a pair of `mirror gambles` between which the agent is not indifferent, we can be sure that they are not indifferent between A and B?

‘Suppose that A and B are consequences between which the agent is not indifferent, and that N is an ethically neutral condition [i.e. the agent is indifferent between N and not N].

Then N has probability 1/2 if and only if the agent is indifferent between the following two gambles:

1. B if N, A if not

2. A if N, B if not’

(Jeffrey, 1983, p. 47)

insert-transcript#afd3c3ac-ad59-429a-be3f-8d29f25bbe4e-here
Suppose that what you get depends on whether you draw a red or white ball from my bucket ...
insert-transcript#2216c88d-3b94-4884-9d19-6877407237e1-here
insert-transcript#d7eab5b7-9096-4569-b142-b44c14769e95-here
Then your indifference between the two doors would allow me to infer that you think there is the same chance of getting either colour or ball.
insert-transcript#af03e02a-d67e-480b-9e51-fd983dd8b601-here

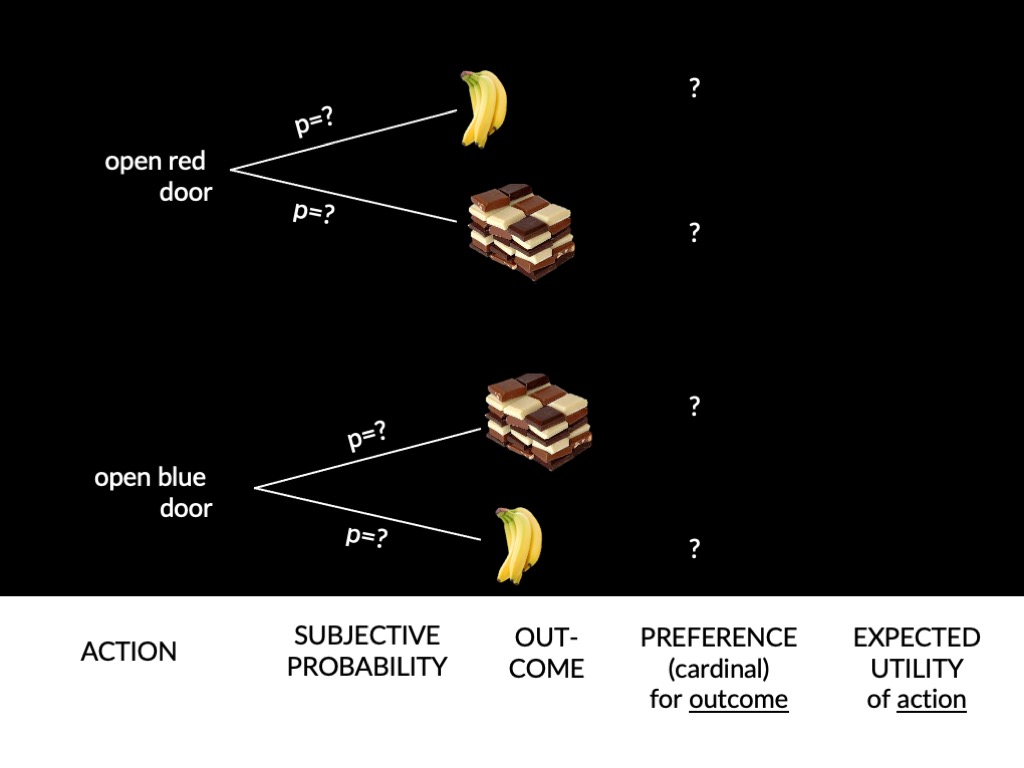
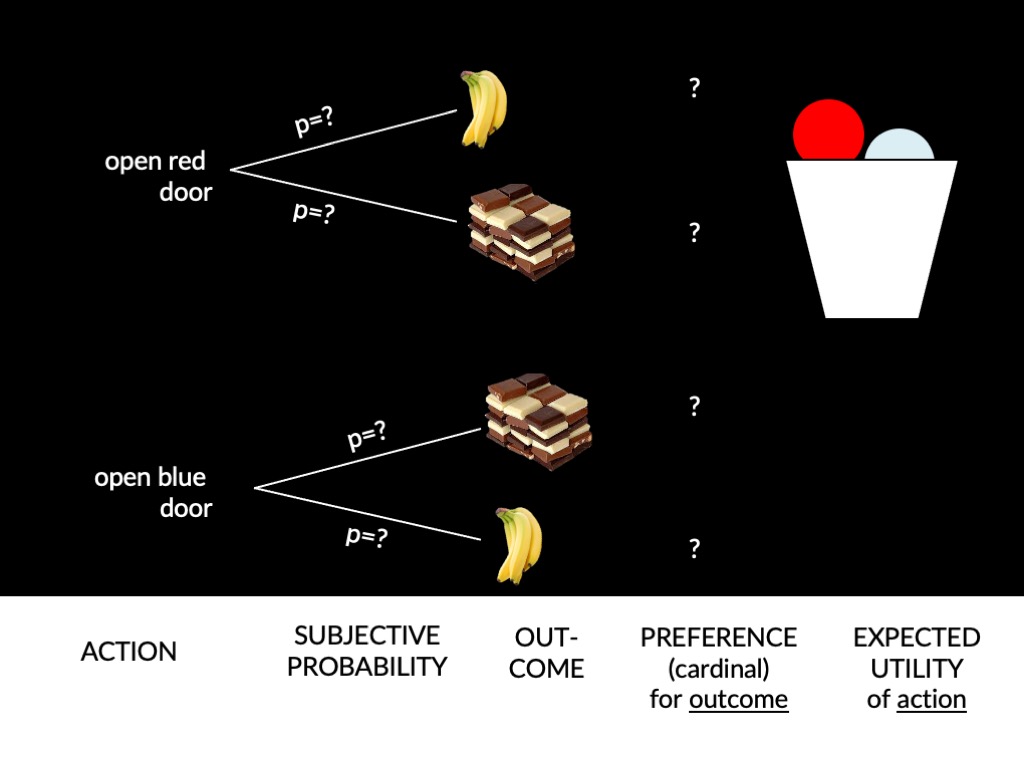
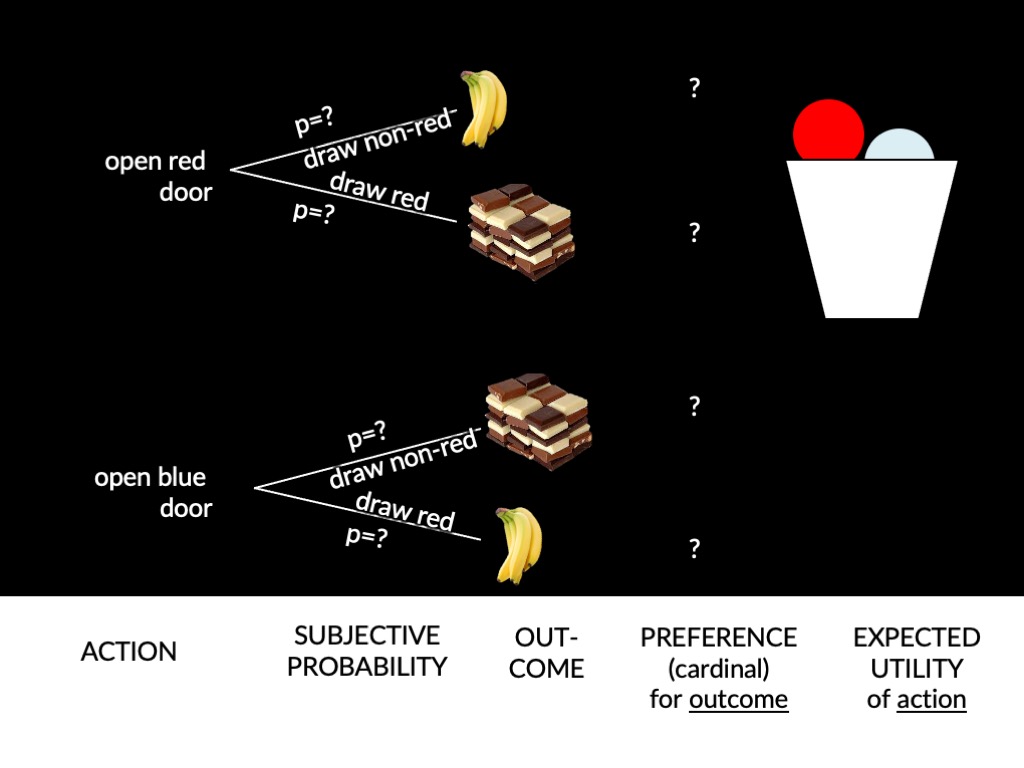
What have we done?

insert-transcript#4b64b54a-1dc3-48f4-a39b-a92e167ce628-here
subjective probabilities and preferences known actions inferred known actions subjective probabilities and preferences inferred

Your actions are a function of two things,
subjective probabilities
and preferences.

Ramsey’s method allows us to
infer both of these
from observations of the actions you perform
plus some background assumptions (axioms).

insert-transcript#9b6d9736-ed06-4e29-810b-0d0d0a4c9397-here
Using Steele & Stefánsson (2020, p. §2.3) here.

But what did we assume in characterising preferences?

transitivity

For any A, B, C ∈ S: if A⪯B and B⪯C then A⪯C.

(Steele & Stefánsson, 2020)

completeness

For any A, B ∈ S: either A⪯B or B⪯A

continuity

‘Continuity implies that no outcome is so bad that you would not be willing to take some gamble that might result in you ending up with that outcome [...] provided that the chance of the bad outcome is small enough.’

Suppose A⪯B⪯C. Then there is a p∈[0,1] such that: {pA, (1 − p)C} ∼ B (Steele & Stefánsson, 2020)

independence

roughly, if you prefer A to B then you should prefer A and C to B and C.

Suppose A⪯B. Then for any C, and any p∈[0,1]: {pA,(1−p)C}⪯{pB,(1−p)C}

Steele & Stefánsson (2020, p. §2.3)

insert-transcript#07373fd6-2a58-4eb5-8938-142e3a49d71b-here

things the theory
assumes

actions

outcomes

+ some axioms (background assumptions)

things the theory characterises

preference

subjective probability

rationality (?!)

insert-transcript#d268c2b4-08ea-4097-abe5-b41072fc35d7-here

This book has ‘a philosophical end: elucidation of the notions of subjective probability and subjective desirability or utility’

(Jeffrey, 1983, p. xi)

The axioms can be regarded as implicitly defining

preference

and

subjective probability.

why necessary?

You might say, I know what these things are.
insert-transcript#2be6db9a-d0a1-490a-892e-36e14cd77ea2-here

1. We as researchers need a shared understanding of belief and desire.

2. There are three potential sources of shared understanding: folk psychology, philosophy and decision theory.

3. Folk psychology does not provide a shared understanding.

4. Nor does philosophy.

Therefore:

5. We need decision theory to provide a shared understanding.

insert-transcript#2fabb765-abf1-4138-8382-7a65bd81e84e-here

This book has ‘a philosophical end: elucidation of the notions of subjective probability and subjective desirability or utility’

(Jeffrey, 1983, p. xi)

‘we should think of
meanings and beliefs
as interrelated constructs of a single theory
just as we already view
subjective values and probabilities
as interrelated constructs of decision theory’

(Davidson, 1974, p. 146)

why necessary?

You might say, I know what these things are.

for shared understanding!

insert-transcript#993cecd5-ec9e-4857-ae1d-f1213a5faaa7-here

so far ...

1. We understand what decision theory is;

2. ... and how it can be used to provide us as researchers with a shared understanding of belief and desire.

3. This is necessary because neither folk psychology nor philosophy provide a shared understanding.

insert-transcript#e5061ade-6cd7-47f2-b498-d0724172161b-here

characterising belief + desire is a problem decision theory offers a solution the dual-proces theory of instrumental action entails that the solution is wrong we cannot use decision theory to characterise belief and desire